Introduction
FALCON is a FEM code written in Fortran90 used to study large-scale geodynamics system, such as continental rifting and subductions. Here you can download the .pdf file with the complete description of all the fetures implemented in the code and all the benchmarks performed. The Gihub repository of this project can be found here and you can download the .zip file containing all of the files at this link.
Table - List of the features implemented in FALCON and of the benchmarks performed.
Features implemented
Governing equations
The code is written in Fortran90 and uses the finite element method (FEM) with quadrilateral Q1×P0 elements (continuous bilinear velocity and discontinuous constant pressure), associated with MUMPS (Amestoy et al., 2001, 2019) that is a software package for solving systems of linear equations by means of a direct method. Since Q1×P0 elements do not satisfy Ladyzhenskaya, Babuska and Brezzi (LBB) stability condition (Donea and Huerta, 2003), elemental pressure is elaborated in post-processing to avoid spurious pressures by means of a double interpolation to smooth the pressure. The thermo-mechanics of crust-mantle systems is described by means of the conservation of mass, momentum and energy equations. The time step dt is chosen in according to Courant-Friedrichs-Lewy condition (Anderson, 1995).
Lagrangian markers
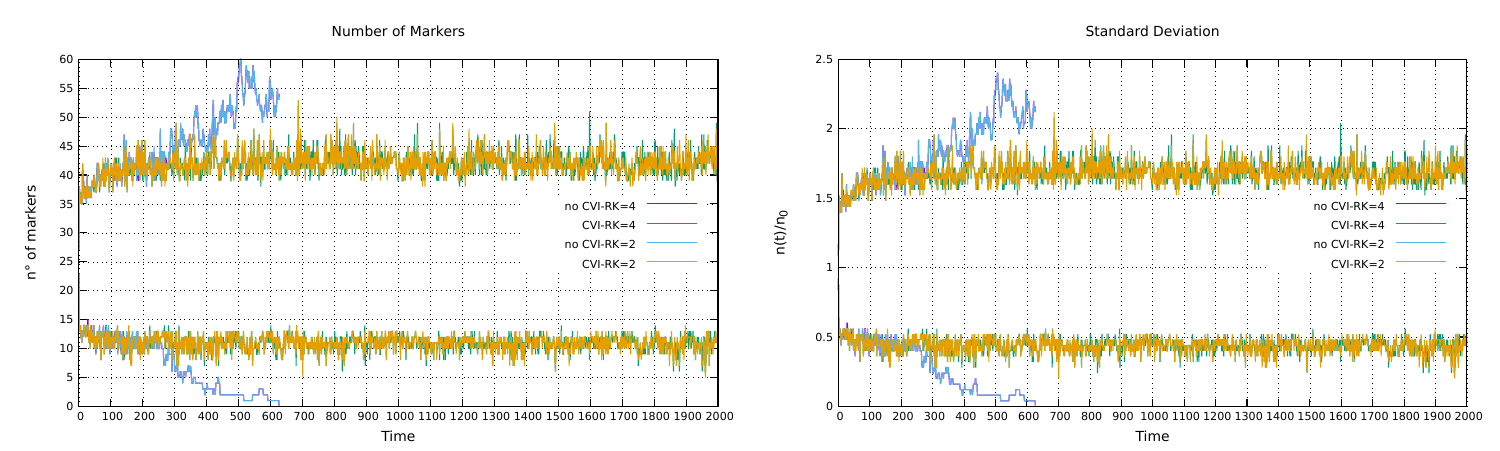
Elemental properties (density, viscosity, thermal conductivity, specific heat and thermal expansion) are related to the composition of each element, determined by means of Lagrangian markers that are characteristic of different materials in the domain. The advection of the markers is performed by either a 2nd-order or a 4th-order Runge-Kutta in space, interpolating the velocity field on each marker by means of the shape functions. The interpolated velocity is then corrected by means of the Conservative Velocity Interpolation (CVI; Wang et al., 2015). The initial distribution of the markers is created using the open-source code library Geodynamic World Builder (Fraters et al., 2019). During the simulation, each marker carries memory of temperature, pressure and accumulated strain and the number of markers contained in each element is maintained between a minimum and a maximum by adding or deleting random markers inside the elements. In this way elements are never empty and maintain a number of markers inside a prefixed range.
Momentum and energy equations
The code implements a so-called penalty formulation for which the flow is not truly incompressible but very weakly compressible. This allows to eliminate the pressure from the momentum equation that is then solved for the velocity field, while the pressure can be recovered as a post-processing step. One strong requirement is that the penalty coefficient λ must be many orders of magnitude larger than the dynamic viscosity η (typically between 5 and 8 orders of magnitude).
The stabilisation of the advection term of the energy equation, needed to avoid possible oscillations in the thermal solution in the case when advection dominates over diffusion, is implemented by means of a streamline-upwind Petrov–Galerkin (SUPG) method, for which the advection term is modified follows the discussion in Thieulot (2011) and Thieulot (2014).
Non-linear rheologies
Non-linear rheologies are implemented combining viscous creep (dislocation and diffusion) and plastic yielding. The viscous creep ηcp is calculated as the harmonic average between ηdf and ηds, while the plastic yielding is implemented rescaling ηcp in order to limit the stress below the yield stress σy determined following the Drucker-Prager criterion. Plastic yielding and viscous creep are then combined to obtain a viscoplastic viscosity ηvp assuming that they are independent processes and the effective viscosity ηeff is capped by the minimum and the maximum viscosity to avoid extremely low or high viscosities. Viscous creep and plastic yielding are non-linear rheologies because of their dependence on the velocity field through pressure and strain rates. Therefore, the solution is determined by means of Picard-type iterations, until convergence of the velocity field. The temporal evolution of the accumulated strain ϵ has been implemented as in Fuchs and Becker (2019, 2021). Strain softening is taken into account for both viscous creep and plastic viscosity by means of the accumulated strain ϵ memorised by each marker. Softening in the viscous creep determines a linear decrease of ηvc by means of a viscous strain softening factor WS, while plastic softening is simulated with a linear decrease of internal friction angle ϕ(ϵ) and cohesion C(ϵ).
Sticky air and free surface
The Earth’s surface can be treated by means of either the so-called sticky-air or a true free surface method, both of them implemented in the code. In the sticky-air method the surface is approximated with the introduction of a buoyant layer with a viscosity at least four orders of magnitude lower than the crust (Schmeling et al., 2008; Crameri et al., 2012) and the interface between lithosphere and air is defined using a chain of passive markers that are advected as the Lagrangian markers. In the true free surface case the top boundary is assumed stress-free and velocities are not fixed. In this case topography variations are described by vertical deformations of the mesh that depend on the velocity field of the nodes that identify the free surface, while horizontal deformations are not taken into account. This procedure is known as the Arbitrary Lagrangian-Eulerian (ALE) method and its implementation follows the technique described in Thieulot (2011) . The stability algorithm proposed by Kaus et al. (2010) is implemented to avoid instabilities due to high density differences at the free surface when using too large time steps.
Phase changes and hydration
Variations of effective density, specific heat and coefficient of thermal expansion during the evolution of crustal and mantle materials at different pressure-temperature (p-T) conditions are computed by means of Perple_X software package (Connolly, 2005). In the case that hydration is switched on, the amount of bound and free water is memorised by each marker, following the implementation of Quinquis and Buiter (2014); hydration and dehydration processes are related to the amount of bound water of each marker and to the maximum amount of water it can transport, i.e. if the amount of bound water exceeds the maximum amount of water, the marker dehydrates and releases free water that can hydrates under-saturated markers. Bound water is advected together with the markers, neglecting the effect of bound water diffusion, while free water simply migrates vertically and is not coupled to the solid-phase flow of the mantle wedge.
Mantle melting
Melt fraction in the mantle depends on temperature (T), pressure (p) and the water content in the melt (in wt.%). The determination of the melt fraction is implemented as explained by Katz et al. (2003). In case of melting, viscous creep viscosity and effective density are modified according to Wang et al. (2016).
Benchmarks
This is a brief description of the benchmarks performed to verify that FALCON correctly solves a wide range of problems, as in the Table below. The Gihub repository with the results of all the benchmarks can be found here. You can download the .zip file containing all the raw data at this link.
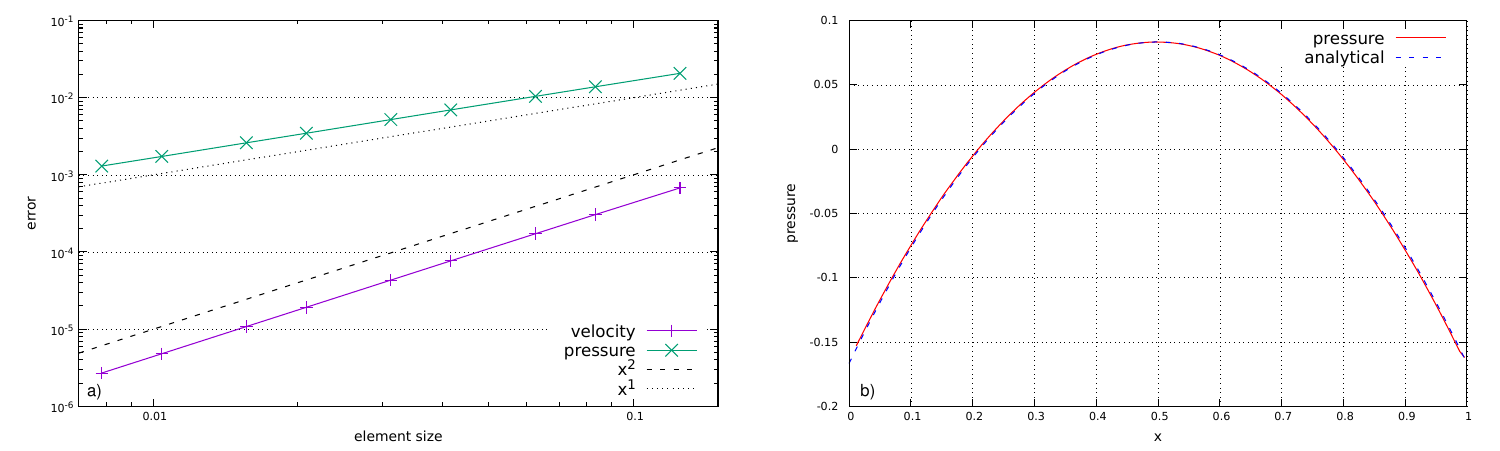
Stokes flow
This experiment is performed as explained by Donea and Huerta (2003). The problem consists of determining velocity field (u, v) and pressure p in case of a manufactured solution with prescribed body forces. The domain is a unit square a constant viscosity and the penalty parameter is set to 107. Velocity boundary conditions are set to no slip (v=0) on all boundaries. The problem is performed for different grid resolution between 8×8 and 1024×1024 elements.
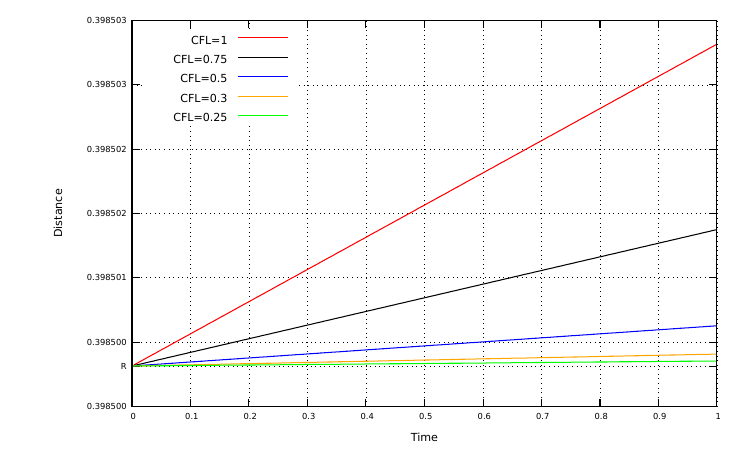
Zalesak disk
This experiment is performed as explained by Zalesak (1979). The benchmark is performed in a unit square domain with a grid resolution of 32×32 elements and values of Courant number (CFL) between 0.25 and 1. The velocity field is prescribed in the entire domain. At t=0, the disk is centred at position (0.5; 0.75) with a radius R=0.15 and has a vertical fissure 0.05 wide and 0.2 high.
Conservative Velocity Interpolation
The Conservative Velocity Interpolation (CVI) correction is checked by means of the Stokes flow experiment, as explained in FIELDSTONE (Stone 30). The advection of Lagrangian markers is performed using either a 2nd-order or a 4th-order Runge-Kutta scheme with CFL=0.5 and an initial random distribution of 25 markers per element.
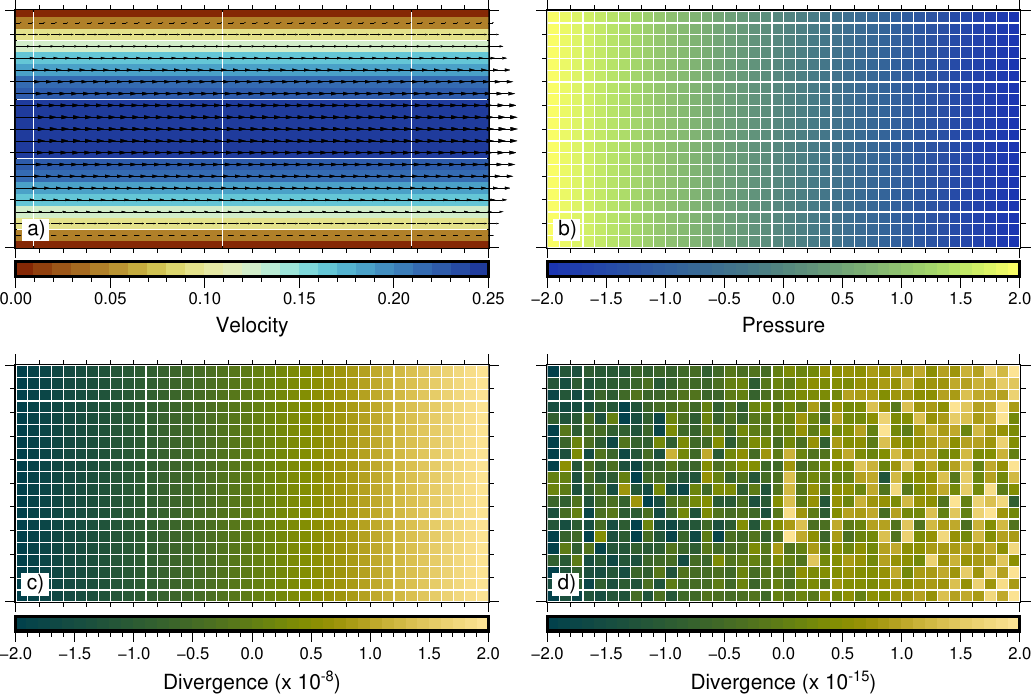
Poiseuille flow
This experiment is performed as explained by Thieulot (2014). The domain is a rectangle with Lx=2 and Ly=1, constant density and viscosity, gravity acceleration equal to 0 and the penalty parameter is 108. The grid is composed by 40×20 elements. Velocity boundary conditions are set to no slip (v=0) at the top and the bottom, and a parabolic profile is imposed on the sides, with vx=y(1−y) and vy=0.
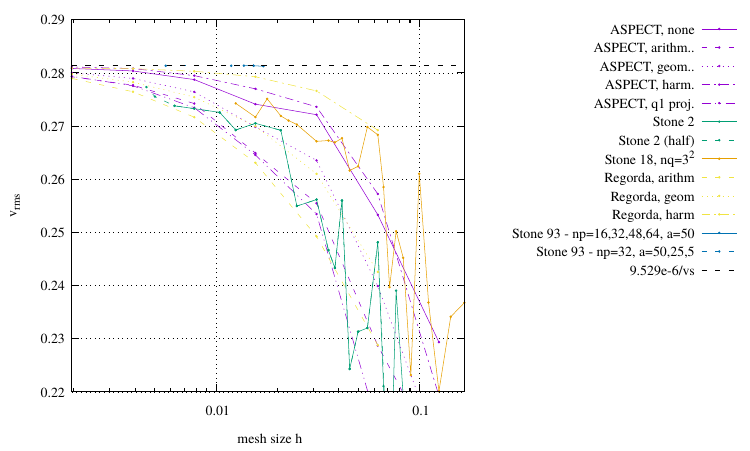
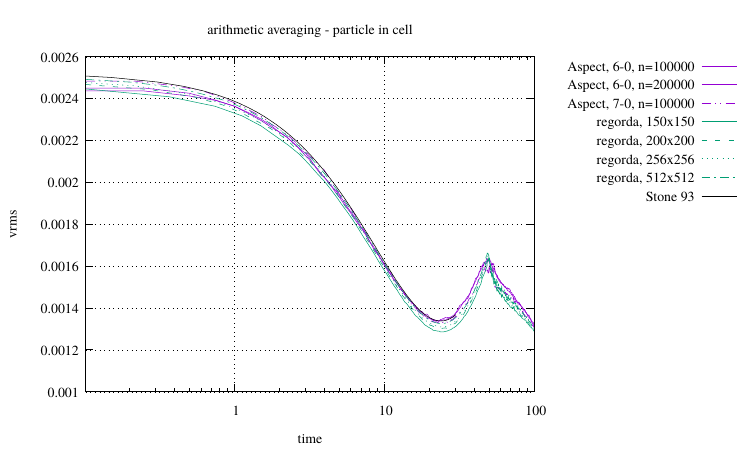
Instantaneous 2D sphere
The experiment is performed as explained in FIELDSTONE (12.2.22). The domain is a unit square with gravity equal to -1. The fluid has constant density and viscosity. The sphere is in the middle of the domain with a radius R=0.123456798 with constant density and viscosity higher than the fluid. Different types of velocity boundary conditions have been tested with grid resolutions between 16×16 and 512×512 elements and different average schemes for the viscosity (harmonic, geometric and arithmetic).
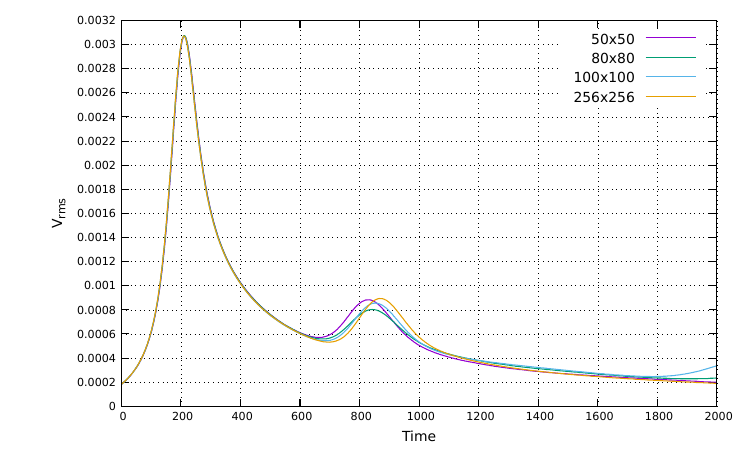
Rayleigh-Taylor experiment
This experiment is performed as explained by Van Keken et al. (1997). The domain has Lx=0.9142 and Ly=1 and gravity equal to -1. Two fluids with same constant viscosities and different densities are distributed in the domain, with the lighter fluid at the bottom. The initial interface between the fluids is given by y(x)=0.2+0.02 cos(πx Lx). The experiment is performed with grid sizes between 50×50 and 256×256 elements. Velocity boundary conditions are set to no slip at the top and the bottom, and to free slip at the sides of the domain.
Falling block
This experiment is performed as explained by Gerya and Yuen (2003) and Thieulot (2011). The domain is square with Lx=Ly= 500 km and the grid is composed by 50×50 elements with 25 markers in each element. The block is initially centred at x=250 km; y=400 km and has a size of 100×100 km. The fluid surrounding the block has constant viscosities and densities. The benchmark tests with different viscosities and densities of the block, with higher density than the surrounding fluid. Velocity boundary conditions are set to free slip conditions on all sides of the domain.
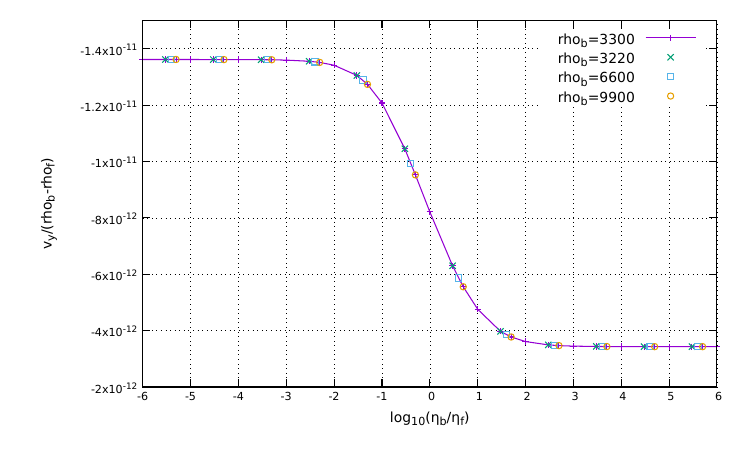
2D Stokes sphere
This experiment is performed as explained in FIELDSTONE (12.2.23), in a unit square domain with the gravity acceleration fixed to −1. The sphere has constant densities and viscosities hogher than the surrounding fluid and it is initially centred at (0.5; 0.6) with radius R = 0.123456789. The fluid surrounding the sphere occupies the domain for y≤0.75, while for y>0.75 there is air. Velocity boundary conditions are set to free slip on all sides. The Courant number is set to 0.25. The experiments run for 200 s using grid resolutions from 150×150 to 512×512 elements, with 25 randomly distributed markers per element, and for different average schemes for the viscosity. The interface between the fluid and the air is tracked by means of the markers chain.
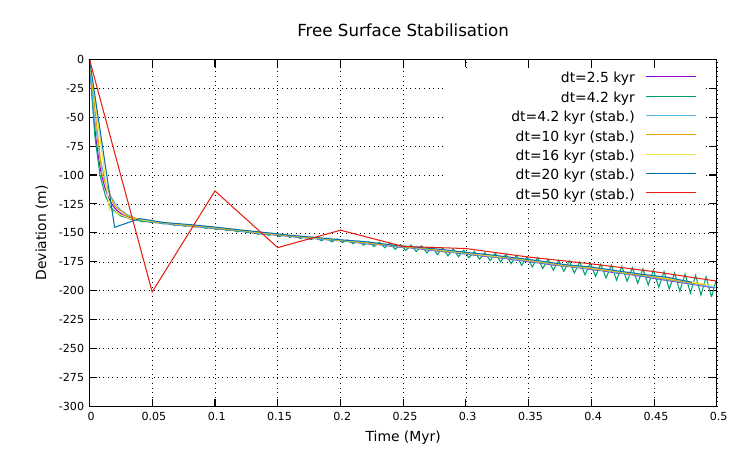
Stabilisation algorithm
This experiment is performed as explained by Kaus et al. (2010). The domain is square with Lx=Ly=500 km and a grid resolution of 200×200 elements, each of them containing 16 markers. A buoyant fluid is overlain by a denser fluid. The initial interface between the fluids has an initial sinusoidal shape of 5 km amplitude. Velocity boundary conditions are set to free slip conditions at the sides and no slip at the bottom, while the top is free surface. The experiment is performed with various fixed time steps.
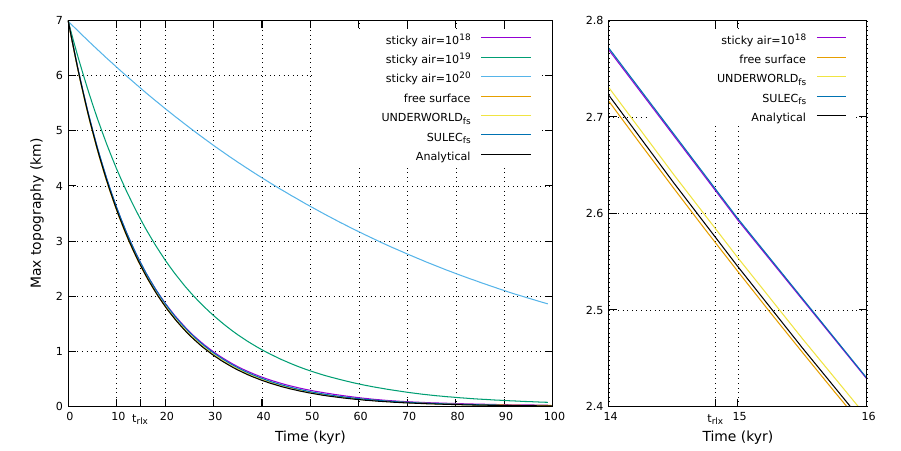
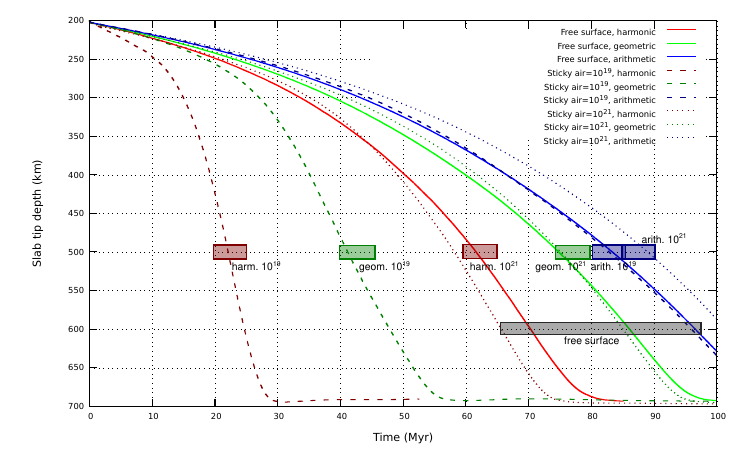
Topography relaxation
This experiment is performed as explained by Crameri et al. (2012). The domain is rectangular with Lx=2800 km and Ly=700 km in case of free surface and Ly=800 km in case of sticky air. The grid is composed by 256×64 elements for the free surface 560×320 elements for the sticky air. For both cases, there is a mantle of 600 km thickness overlain by a highly viscous cosine-shaped lithosphere with thickness between 93 and 107 km. Velocity boundary conditions are set to no slip at the bottom and free slip at the sides of the domain. In case of sticky air, velocities on top are set to free slip conditions.
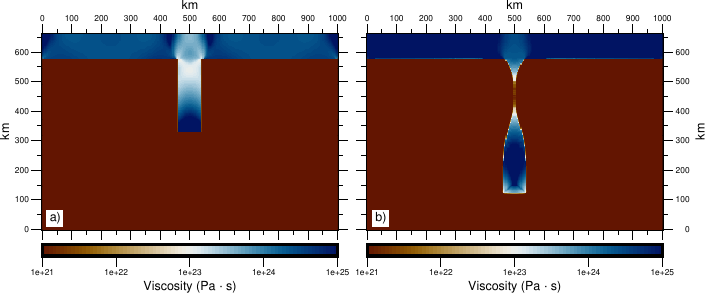
Spontaneous subduction
This experiment is performed as explained by Schmeling et al. (2008), with both a sticky air and a true free surface and using different average schemes for the viscosities. The domain is rectangular with Lx=3000 km and Ly=700 km, a grid resolution of 256×64 elements with 50 markers per element and Courant number of 0.01. At the beginning of the simulation, a denser 100 km-thick lithospheric layer is located at the top of the domain for x between 1000 and 3000 km. In addition, a 200 km-depth lithospheric slab is already subducted in the mantle in order to have a spontaneous subduction. In case of sticky air, a 50 km-thick air layer overlie the mantle. Velocity boundary conditions are set to free slip on the sides and on the bottom of the domain. In case of sticky air, velocities on the top boundary are set to free slip conditions as well.
Slab detachment
The slab detachment benchmark is performed as explained by Schmalholz (2011) and Glerum et al. (2018). The domain is rectangular with Lx=1000 km and Ly=660 km and a grid resolution of 256×256 elements. A denser non-linear viscous T-shaped layer is placed at the top of the domain and surrounded by a linear viscous fluid. The top layer is 80 km-thick and a 250 km-long and 80 km-wide slab is placed at x=Lx/2. Velocity boundary conditions are set to free slip at the top and the bottom, and to no slip at the sides of the domain.
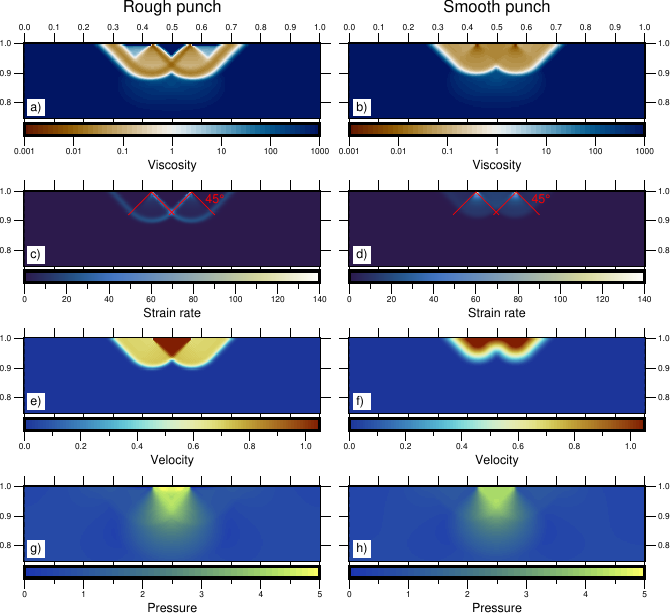
Indenter
The indenter benchmark is performed as explained by Thieulot et al. (2008) and Glerum et al. (2018). The indenter benchmark simulate a rigid punch on a purely plastic von Mises material, for which exists an analytical solution. The domain is a unit square with a grid resolution of 256×256 elements. The gravity acceleration is set to 0. Velocity boundary conditions are set to no slip at the bottom and free slip at the sides of the domain. The top of the domain is open with the exception of the central portion (punch area) with width wp=0.125, where vy= −1.05 and vx is fixed either to 0 (rough punch experiment) or free (smooth punch experiment).
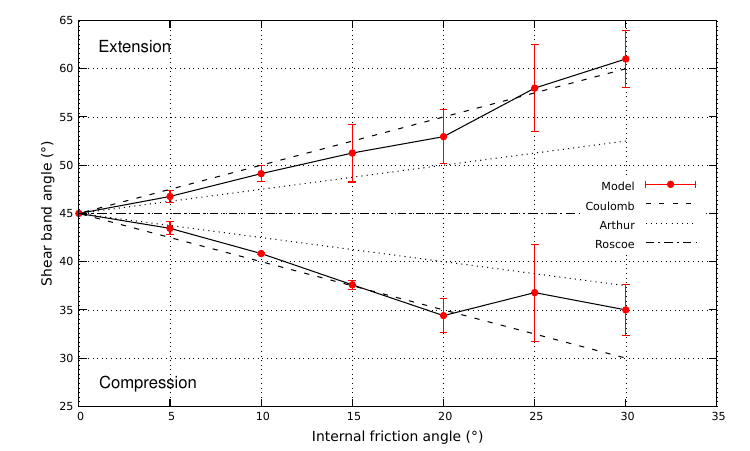
Brick
The experiment is perfomed as explained by Glerum et al. (2018) to verify the correctness of the pressure-dependent plasticity for different angle of internal friction. The domain is rectangular with Lx=40 km and Ly=10 km and a grid resolution of 512×128 elements. The maximum number of non-linear iterations is set to 1000. A 800 m-wide and 400 m-height inclusion is placed at the bottom of the domain at x=Lx/2. The inclusion is surrounded by a non-linear viscous medium. Velocities are set to free slip conditions at the bottom of the domain and the top is open. Velocities on sides of the domain are fixed to vx=±2×10−11 m s−1 and vy=0. The experiment is performed in compressional and extensional contexts with an angle of internal friction of the non-linear medium variable between 0° and 30°.
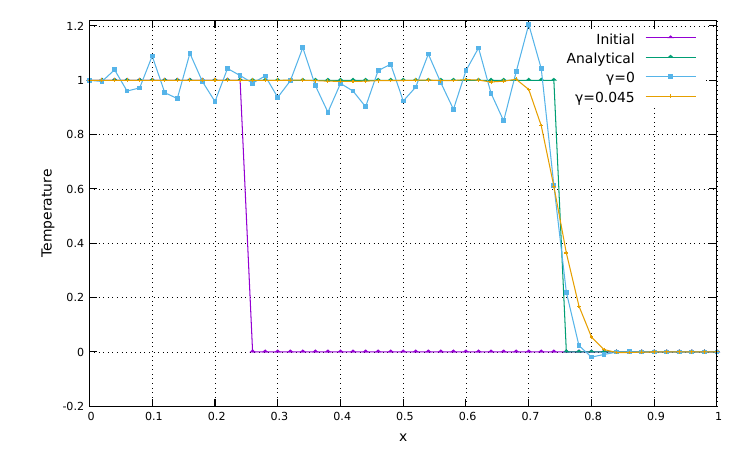
Advection stabilisation
The 1D advection problem proposed by Donea and Huerta (2003) and Thieulot (2011) is performed to verify the effectiveness of the SUPG method to stabilise the advection term of the energy equation. The domain is a 1D segment with Lx=1 composed by 50 elements and a discontinuity in the thermal field placed at x=0.25. Temperature is set to 1 for x ≤ 0.25 and to 0 for x > 0.25. Velocity is set to ux=1 in the entire domain. The simulation is performed for 250 time steps, with dt = 0.002, so the thermal discontinuity should be at x = 0.75 at the end of the simulation. Temperature profiles at the end of the simulation are function of the dimensionless coefficient γ = τux/h.
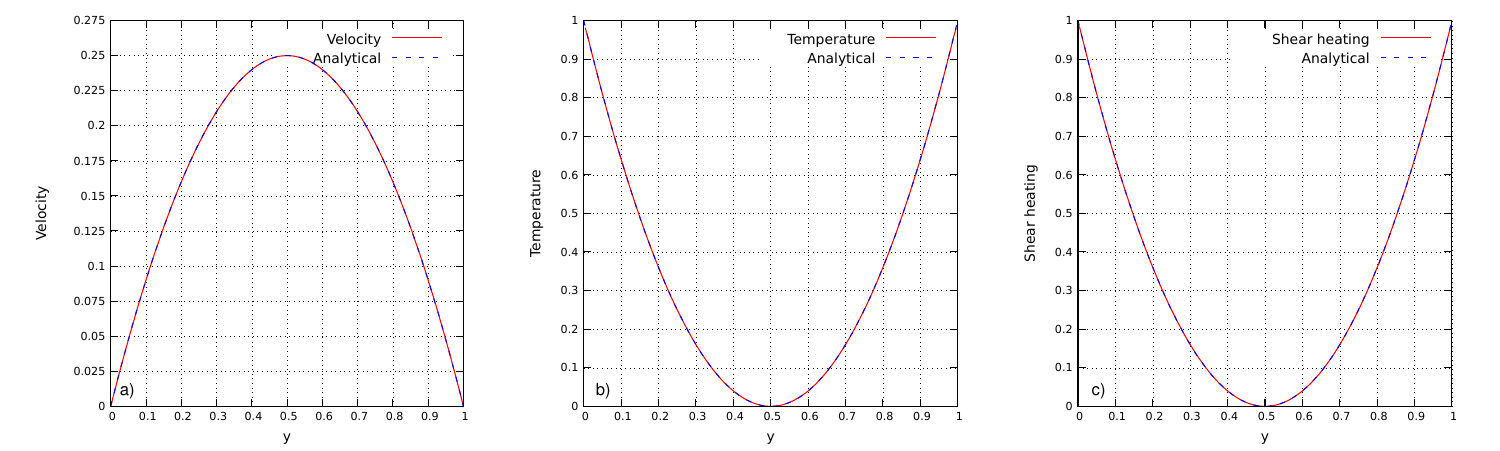
Simple shear heating
This exercise is performed in an unit square domain composed by 128×128 elements. The velocity field is prescribed on the entire domain with ux=(Ly−y)y; viscosity, density and specific heat are fixed to 1, while thermal conductivity and radiogenic energy are fixed to 0. Therefore, the energy equation can be simplified and fixing T(t=0)=0, the temperature can be find as T(t)=Hst, where shear heating Hs can be calculated as Hs(x,y)=(1−2y)2.
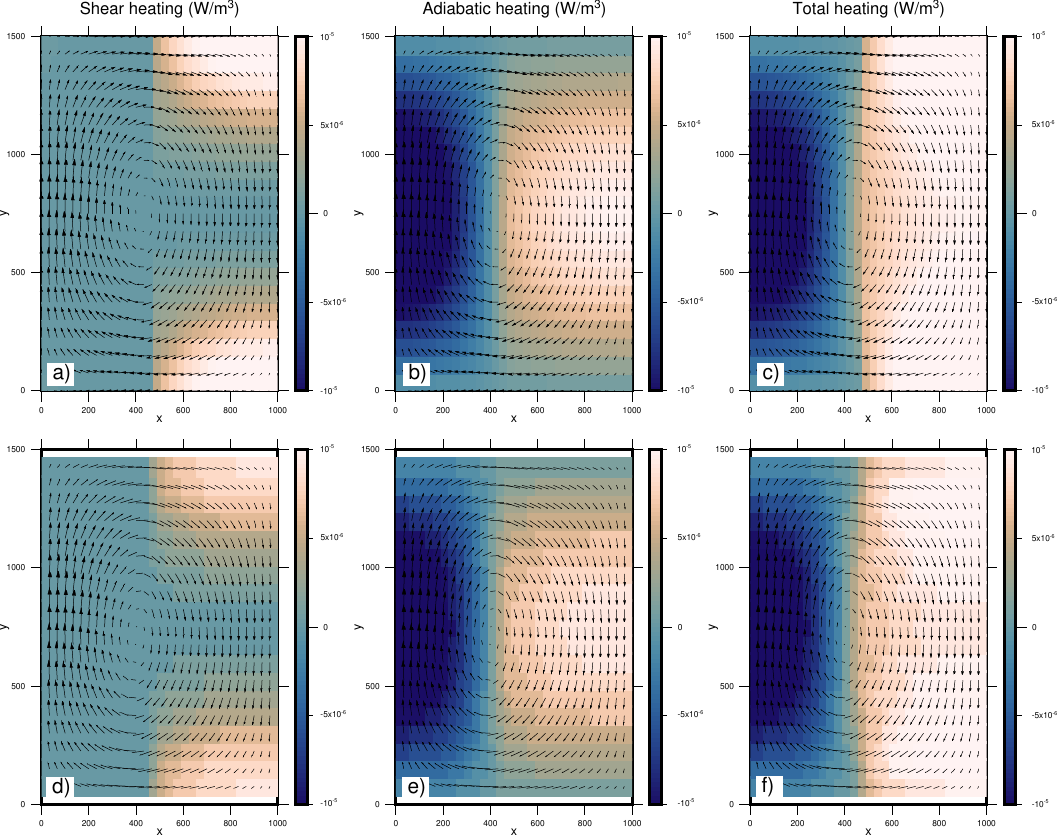
Shear and adiabatic heating
This problem is performed as presented in Exercise 9.4 in Gerya (2010). Two materials are vertically separated in a rectangular domain with Lx=1000 km, Ly=1500 km and a grid resolution of 30×20 elements. Constant thermal coefficient expansion (α=3×10−5 K−1), temperature (T=1300 K) and gravity acceleration (gy=−10 ms2) are assumed in the whole domain. Fluid 1 on the left side of the domain has lower densitiea nd viscosities with respect to fluid 2 on the right side of the domain. Velocity boundary conditions are set to free slip on all sides of the domain.
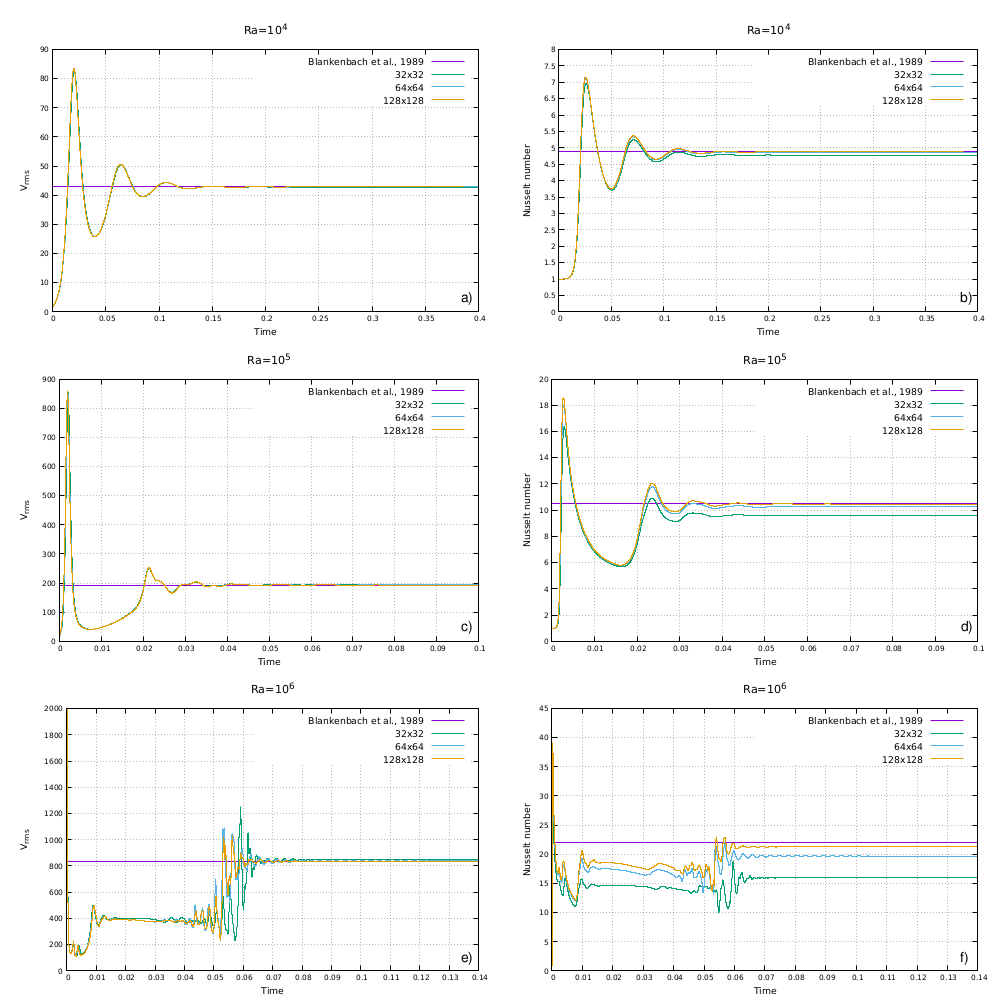
Mantle convection
This problem is performed as presented by Blankenbach et al. (1989)(constant viscosity cases), in a 2D unit square domain with gravity acceleration gy = 1010Ra. The experiment is performed with three different Rayleigh numbers (Ra=104, 105 and 106) and with different grid resolution (between 32×32 and 128×128 elements). The fluid has constant viscosity, initial density, heat capacity, thermal conductivity (η =ρ0=Cp=k=1), reference temperature (T0=0) and thermal expansion coefficient (α=10−10). Temperatures are set to 0 on top and 1 on bottom of the domain. Velocity boundary conditions are set to free slip on all sides. The initial temperature field is given by T(x,y)=(1−y)+0.01 cos(πx) sin(πy).
Visco-plastic mantle convection
This benchmark is performed as Cases 1-5a described in Tosi et al. (2015) in a 2D unit square domain with two different grid resolutions of 32×32 and 100×100 elements. Reference viscosity, reference density, heat capacity, thermal conductivity and thermal expansion coefficient are fixed to a constant value of 1 (η0=ρ0=Cp=k=α=1), while the gravity has been chosen as gy=102, in order to obtain a Rayleigh number Ra=102. Temperatures are set to 0 on top and 1 on bottom of the domain. Velocity boundary conditions are set to free slip on all sides. The initial temperature field is given by T(x,y)=(1−y)+0.01 cos(πx) sin(πy) The viscosity field η is calculated as the harmonic average between a linear part ηlin that depends on temperature only or on temperature and depth y and a nonlinear-plastic part ηpl that depends on the strain rate ϵ̇. See Tosi et al. (2015) for more details.
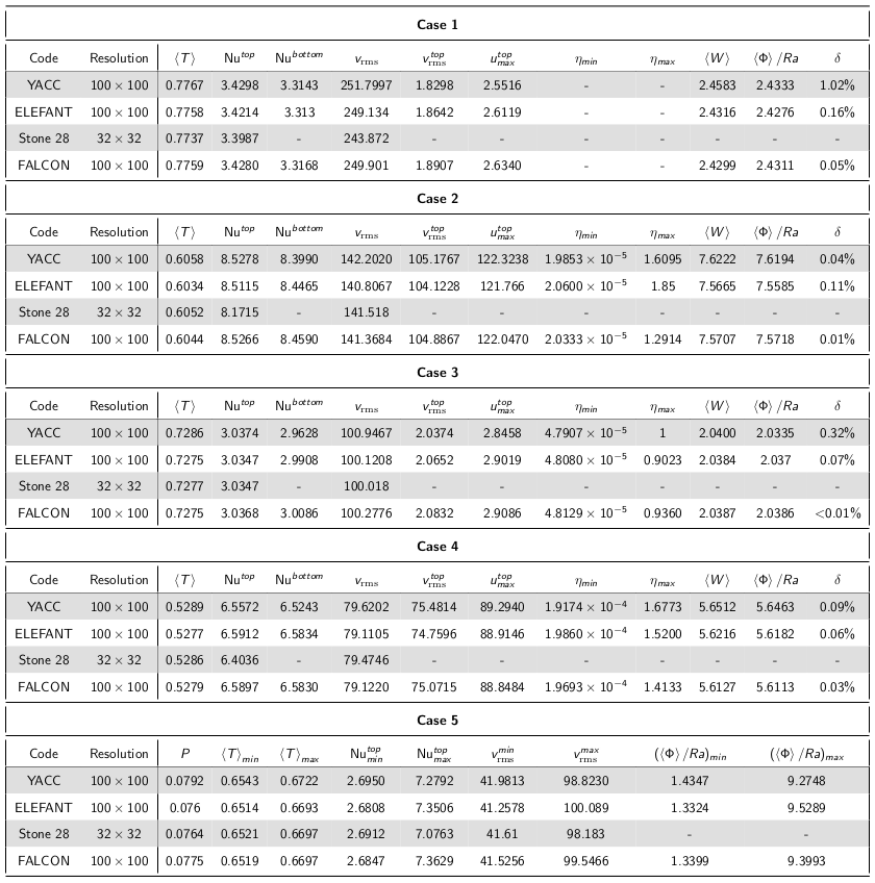
Thin layer entrainment
This experiment is performed as originally proposed by Van Keken et al. (1997) with two incompressible fluids in a rectangular domain with Lx=2 and Ly=1 and gravity acceleration gy=1010 Ra. The Rayleigh number and the compositional Rayleigh number are fixed to Ra=300000 and Rc=450000, respectively. Both fluids have constant viscosity, thermal conductivity, specific heat (η=ρ=Cp=1) and thermal expansion coefficient (α=10−10). Fluid 1 has a density ρ1=1, while fluid 2 is denser (ρ2=ρ1+1.5·10−10) and is placed at the bottom of the domain, for y≤0.025. Temperature are set to 0 on top and 1 on bottom of the domain. Velocity boundary conditions are set to free slip on all sides of the domain. See Van Keken et al. (1997) for details about the initial temperature field. The experiment is performed with two grid resolution (125×40 and 200×80 elements), with 100 markers per element and Courant number of 0.25.
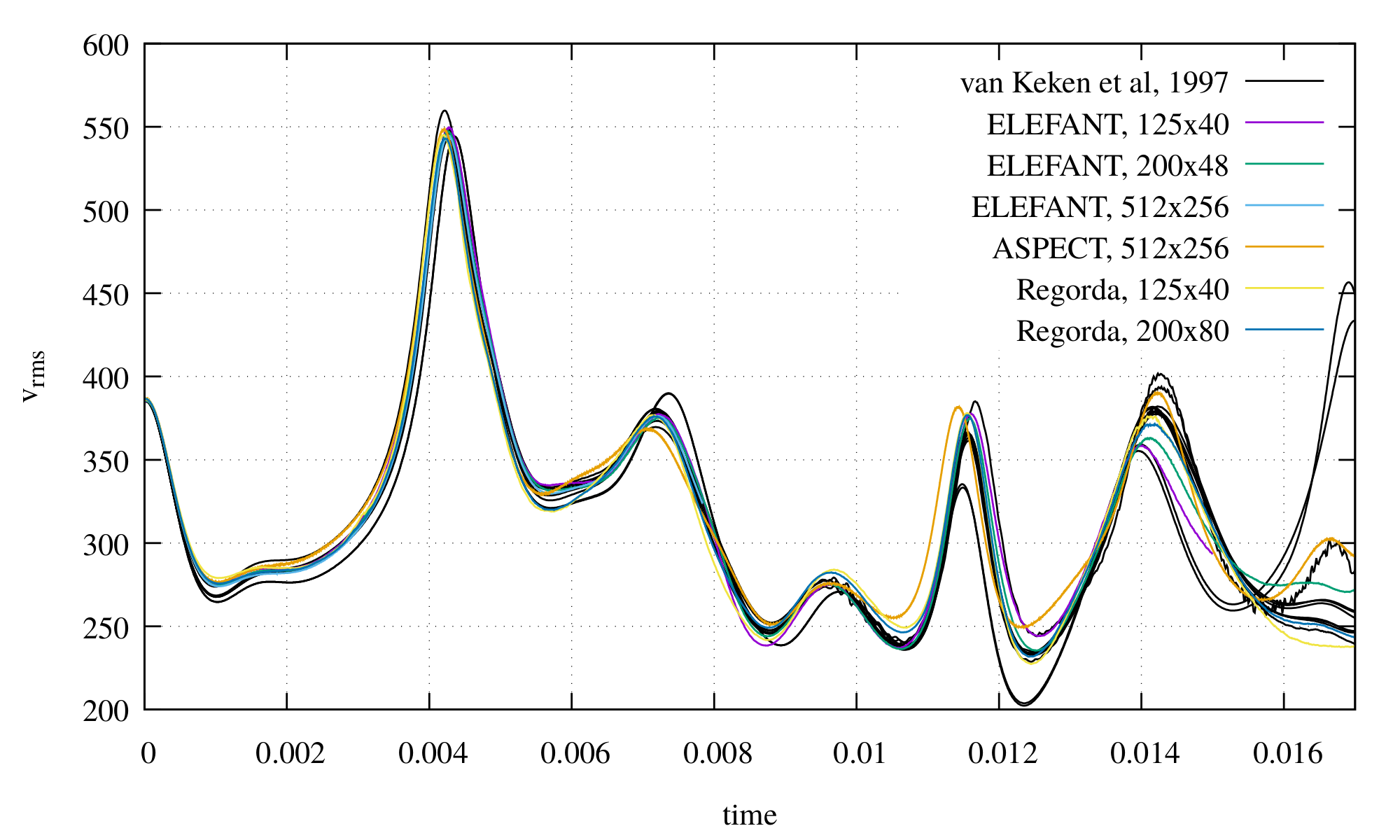
Hydrated sinking cylinder
This experiment is performed as explained in Quinquis and Buiter (2014) and simulates the sinking of a cold, hydrated cylinder into a warm, dry mantle. The domain is square with Lx=Ly=300 km, a grid resolution of 300×300 elements and 25 markers per element. The sinking cylinder is located at x=150 km and y=170 km with a radius of 20 km and has ρc=3250 kg m−3,ηc=1×1023 Pa s, a thermal conductivity kc=4.5 W m−1 K−1, a specific heat Cpc=1250 J kg−1 K−1; the surrounding mantle has ρm=3200 kg m−3, ηm=1×1020 Pa s, a thermal conductivity km=105 W m−1 K−1 and specific heat Cpm=1250 J kg−1 K−1; a 58 km-thick lithosphere overlies the mantle and has ρc=3200 kg m−3, ηl=1×1023 Pa s, a thermal conductivity kl=4.5 W m−1 K−1, Cpl=750 J kg−1 K−1 and a thermal diffusivity of 1×10−6 m2 s−1. Velocity boundary conditions are set to free slip on all sides of the domain. Temperature increase linearly in the lithosphere, from 0° to 1300°C, and in the mantle, from 1300° to 1360.5°C. The initial temperature of the cylinder is fixed to 400°C. Throughout the evolution, temperature is fixed to 0° and 1360.5°C at the top and bottom of the domain, respectively. The initial bound water content is imposed at 2 wt.% in the cylinder and at 0 wt.% in both the mantle and the lithosphere. The maximum amount of water in the mantle is fixed to 0.2 wt.%, while maximum water content in the cylinder and in the lithosphere is function of pressure and temperature and is calculated using a serpentinized harzburgite with Perple_X, as in Quinquis and Buiter (2014).
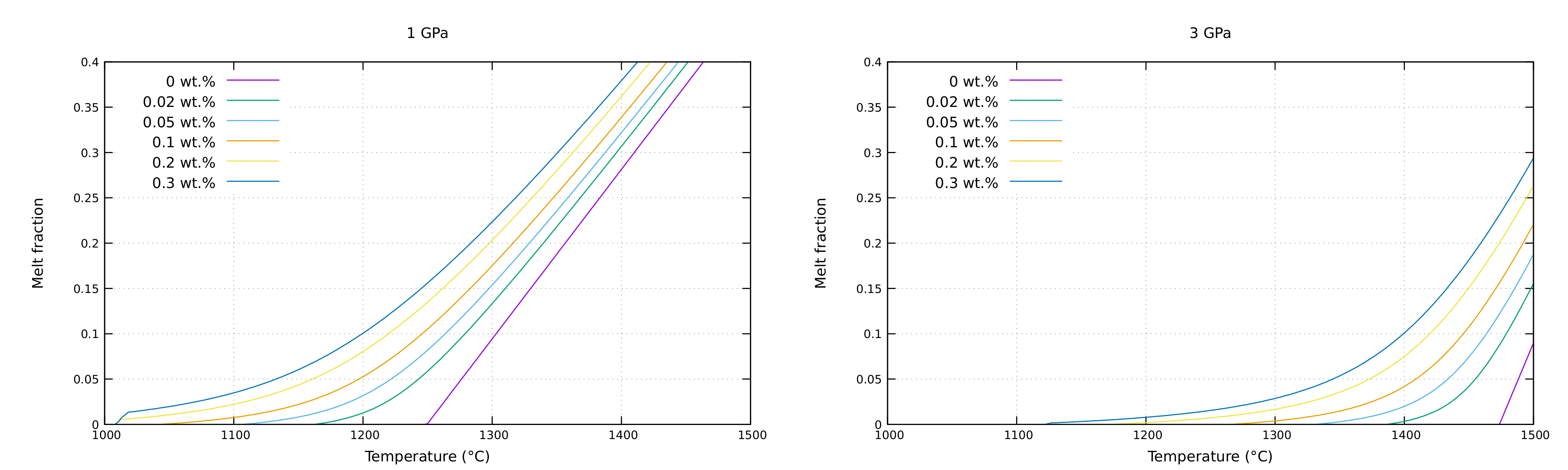
Experimental melting curves
This instantaneous experiment is performed in order to recreate isobaric melting curves, as function of temperature, bulk water and content of water in the melt, to compare with melting curves obtained by Katz et al. (2003). The domain is square with Lx=Ly=100 km, a grid resolution of 100×100 elements and 25 markers per element. Density is set in the entire domain to 3300 kg m−3 and temperature increases from the sides to the centre from 1000° to 1500°C. The experiment is performed for bulk water contents from 0 to 0.3 wt.%.